Skip to main content
Home Peluang Jenis-jenis Bilangan dalam Matematika

Jenis-jenis Bilangan dalam Matematika

Bilangan dalam matematika terdiri dari beberapa tingkatan. Induk dari semua bilangan adalah bilangan komplek. Bilangan komplek ini terdiri dari dua jenis, yaitu bilangan riil dan bilangan imajiner.

Bilangan riil terdiri dari bilangan rasional dan bilangan irasional. Bilangan rasional terdiri dari bilangan bulat dan bilangan pecahan.

Bilangan bulat terdiri dari bilangan negatif dan bilangan cacah, sedangan bilangan pecahan terdiri dari bilangan pecahan murni dan bilangan pecahan campuran.

Selanjutnya bilangan cacah terdiri dari bilangan asli dan bilangan nol.

Secara ringkas jenis-jenis bilangan tersebut dapat digambarkan dalam diagram berikut.

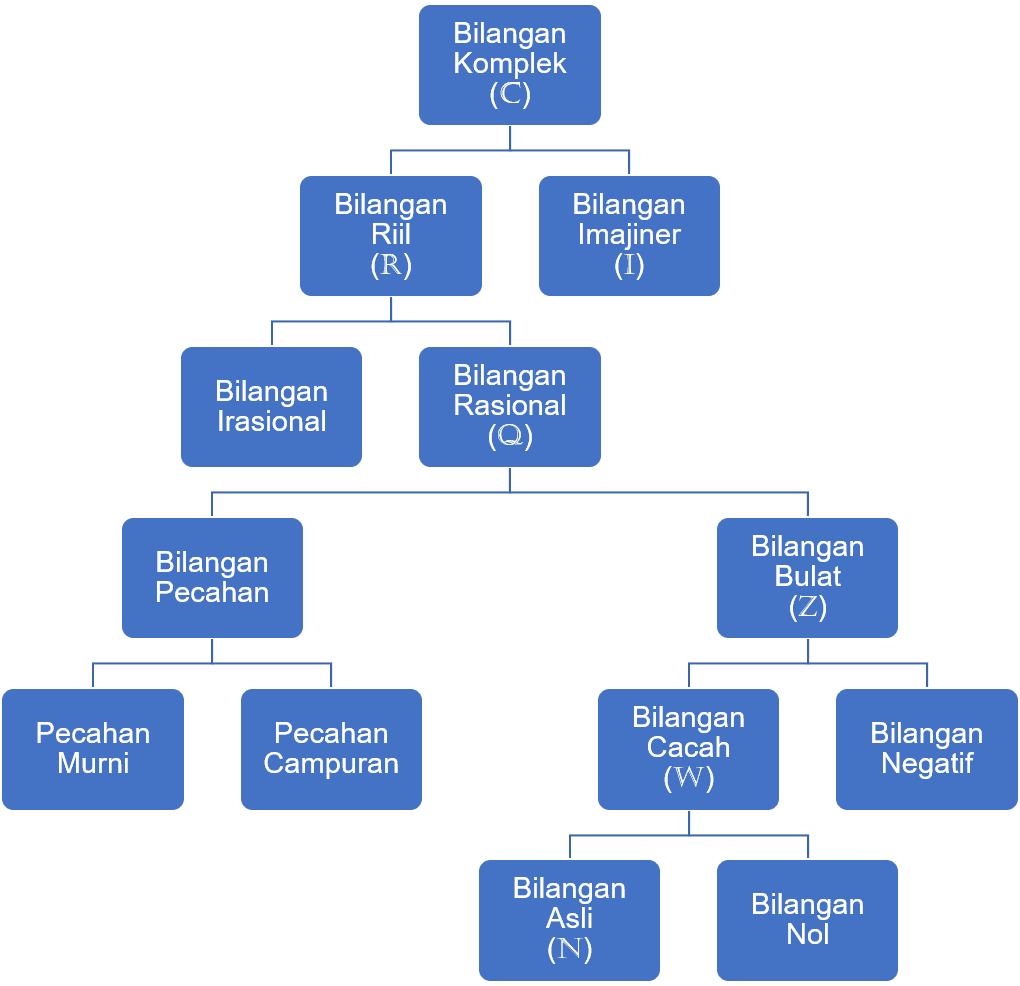
diagram bilangan

Dalam bentuk himpunan, hubungan masing-masing bilangan dimulai dari bilangan riil adalah sebagai berikut.

himpunan bilangan

Penjelasan bilangan-bilangan tersebut adalah sebagai berikut.

Bilangan Asli

Bilangan asli (natural numbers) adalah konsep bilangan yang pertamakali ditemukan dan digunakan dalam rangka melakukan penghitungan dan pengukuran.

Bilangan asli dimulai dari bilangan 1 ke atas dan himpunannya dilambangkan dengan \(\mathbb{N},\) sehingga

\[\mathbb{N} = \{1, 2, 3, \cdots\}\]

Dalam perkembangannya, bilangan asli disebut juga dengan bilangan positif.

Bilangan asli dapat dikelompokkan lagi menjadi bilangan prima dan bilangan komposit.

  1. Bilangan Prima

    2. Bilangan prima adalah bilangan asli (tidak termasuk 1) yang hanya bisa habis dibagi oleh 1 dan bilangan itu sendiri. Bilangan 2, 3, 5 dan 7 adalah bilangan prima karena hanya habis dibagi oleh 1 dan bilangan itu sendiri. Bilangan 4 dan 6 bukanlah bilangan prima karena habis dibagi 2. Himpunan bilangan prima adalah \(\{2, 3, 5, 7, 11, \cdots\}.\)

  2. Bilangan Komposit

    3. Bilangan komposit adalah bilangan asli tidak termasuk 1 yang yang tidak termasuk ke dalam bilangan prima. Himpunan bilangan prima adalah \(\{4, 6, 8, 9, 10, \cdots\}.\)

Bilangan Nol

Bilangan nol adalah bilangan tunggal yang hanya terdiri dari satu bilangan yaitu \(0\) (Nol). Bilangan ini adalah bilangan yang ditemukan setelah munculnya bilangan asli. Munculnya bilangan ini karena kebutuhan manusia terhadap bilangan semakin meningkat.

Bilangan Cacah

Bilangan cacah (whole numbers) adalah gabungan dari bilangan nol dan bilangan asli. Bilangan cacah dilambangkan dengan \(\mathbb{W},\) dimana himpunan

\[\mathbb{W} = \{0, 1, 2, 3, \cdots\}\]

Bilangan Negatif

Bilangan negatif adalah bilangan yang kecil dari 0. Himpunan bilangan negatif adalah \(\{\cdots, -3, -2, -1\}\)

Bilangan Bulat

Bilangan bulat (integers) adalah bilangan yang terdiri dari bilangan asli (bilangan positif), bilangan nol dan bilangan negatif. Bilangan bulat dilambangkan dengan \(\mathbb{Z},\) dimana himpunan \(\mathbb{Z}\) adalah

\[\mathbb{Z} = \{\cdots, -3, -2, 1-, 0, 1, 2, 3, \cdots\}\]

Bilangan bulat dapat dikelompokkan lagi menjadi dua, yaitu bilangan ganjil dan bilangan genap.

  1. Bilangan Ganjil

    2. Bilangan ganjil adalah bilangan bulat yang tidak habis dibagi dua. Himpuan bilangan ganjil adalah \(\{\cdots, -9, -7, -5, -3, -1, 1, 3, 5, 7, 9, \cdots\}.\)

  2. Bilangan Genap

    3. Bilangan genap adalah bilangan bulat yang habis dibagi dua. Himpuan bilangan genap adalah \(\{\cdots, -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, \cdots\}.\)

Bilangan bulat memiliki sifat-sifat sebagai berikut.

  1. Tertutup

    2. Bilangan bulat mempunyai sifat tertutup pada operasi penjumlahan, pengurangan dan perkalian. Misalkan \(a\) dan \(b\) adalah bilangan bulat, maka \(a + b = c,\) \(a - b = d\) dan \(a \times b = e\) dimana \(c,\) \(d\) dan \(e\) merupakan bilangan bulat pula. Bilangan bulat tidak bersifat tertutup pada operasi pembagian.

  2. Komutatif

    3. Bilangan bulat bersifat komutatif untuk operasi penjumlahan dan perkalian. Untuk setiap bilangan bulat \(a\) dan \(b\) akan selalu berlaku persamaan \(a + b = b + a\) dan \(a \times b = b \times a.\)

  3. Asosiatif

    4. Bilangan bulat bersifat asosiatif untuk operasi penjumlahan dan perkalian. Untuk setiap bilangan bulat \(a,\) \(b\) dan \(c\) akan selalu berlaku persamaan \((a + b) + c = a + (b + c)\) dan \((a \times b) \times c = a \times (b \times c).\)

  4. Mempunyai unsur identitas

    5. Bilangan bulat mempunyai unsur identitas pada operasi penjumlahan. Untuk setiap bilangan bulat \(a\) akan selalu berlaku persamaan \(a + 0 = 0 + a = a\) dan \(a \times 1 = 1 \times a = a\) dimana bilangan nol \((0)\) merupakan unsur identitas pada penjumlahan bilangan satu \((1)\) merupakan unsur identitas pada perkalian.

  5. Mempunyai invers

    6. Bilangan bulat mempunyai invers pada operasi penjumlahan. Untuk setiap bilangan bulat \(a\) akan selalu berlaku persamaan \(a + (-a) = (-a) + a = 0,\) sehingga invers dari \(a\) adalah \(-a\) dan invers dari \(-a\) adalah \(a.\)

Bilangan Pecahan

Bilangan pecahan adalah bilangan yang memiliki bentuk \(\displaystyle \frac{a}{b}\) dimana pembilang \(a\) dan penyebut \(b\) adalah bilangan bulat dan penyebut \(b \neq 0.\).

Bilangan pecahan dapat dibagi lagi menjadi dua yaitu bilangan pecahan murni dan bilangan pecahan campuran.

  1. Bilangan Pecahan Murni

    2. Bilangan pecahan murni adalah bilangan pecahan dimana pembilangnya lebih kecil dari penyebutnya, misalnya

    \[\frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{2}{5}, \frac{5}{9}.\]
  2. Bilangan Pecahan Campuran

    3. Bilangan pecahan campuran adalah bilangan pecahan yang pembilangnya lebih besar dari penyebutnya. Jika bilangan tersebut disederhanakan maka bilangan tersebut akan terdiri dari bilangan bulat dan pecahan murni, misalnya

    \[\begin{aligned} \frac{3}{2} &= 1\frac{1}{2}\\ \frac{7}{2} &= 2\frac{1}{3}\\ \frac{15}{4} &= 3\frac{3}{4} \end{aligned}\]

Bilangan Rasional

Bilangan rasional (rational numbers) adalah bilangan yang berbentuk \(\displaystyle \frac{a}{b}\) dimana \(a\) dan \(b\) adalah bilangan bulat dan \(b \neq 0.\) Jika bilangan rasional disederhanakan maka bentuknya adalah bilangan bulat atau bilangan pecahan. Bilangan rasional dapat dinyatakan sebagai suatu bilangan desimal secara berulang. Himpunan bilangan rasional dinotasikan dengan huruf \(\mathbb{Q}.\)

Bilangan Irasional

Bilangan irasional adalah bilangan yang jika dituliskan dalam bentuk desimal, maka hasilnya tidak akan berhenti dan polanya tidak berulang (tidak beraturan) misalnya \(\pi,\) \(\sqrt{2}\) dan \(e.\)

\[\begin{aligned} \pi &= 3\text{,}141592653589793...\\ \sqrt{2} &= 1\text{,}414213562373095...\\ e &= 2\text{,}7182818... \end{aligned}\]

Perbedaan bilangan rasional dan irasional terletak pada hasil desimal tersebut, dimana bilangan desimal yang diperoleh dari bilangan rasional adalah bilangan desimal yang beraturan, misalnya

\[\begin{aligned} \frac{2}{3} &= 0\text{,}6666666666...\\ \frac{15}{11} &= 1\text{,}3636363636...\\ \frac{100}{33} &= 3\text{,}0303030303...\\ \frac{125}{111} &= 1\text{,}1261261261...\\ \end{aligned}\]

Bilangan Imajiner

Bilangan imajiner (imaginary numbers) adalah bilangan yang ketika dikuadratkan akan menghasilkan nilai negatif yaitu seperti \(i^2 = -1\) atau \(i = \sqrt{-1}.\) Bilangan imajiner dinotasikan oleh \(\mathbb{I}.\)

Contoh bilangan imajiner adalah \(5i,\) \(1\text{,}25i,\) \(\frac{1}{4}i,\) dan \(\sqrt{3}i.\) Adanya notasi \(i\) menyatakan bahwa bilangan-bilangan sebelumnya perlu dikalikan dengan \(\sqrt{-1}.\)

Bilangan Riil

Bilangan real (ral numbers) adalah bilangan yang dibentuk dari bilangan rasional dan bilangan irasional. Himpunan bilangan riil dinotasikan dengan \(\mathbb{R}.\)

Sifat-sifat bilangan riil adalah sebagai berikut.

  1. Komutatif

    2. Bilangan riil bersifat komutatif untuk operasi penjumlahan dan perkalian. Untuk setiap bilangan riil \(a\) dan \(b\) akan selalu berlaku persamaan

    \[\begin{aligned} a + b = b + a \\ a \times b = b \times a \end{aligned}\]
  2. Asosiatif

    3. Bilangan riil bersifat asosiatif untuk operasi penjumlahan dan perkalian. Untuk setiap bilangan riil \(a,\) \(b\) dan \(c\) akan selalu berlaku persamaan

    \[\begin{aligned}(a + b) + c = a + (b + c) \\ (a \times b) \times c = a \times (b \times c) \end{aligned}\]
  3. Distributif

    4. Untuk setiap bilangan riil \(a,\) \(b\) dan \(c\) akan selalu berlaku persamaan

    \[\begin{aligned} a \times (b + c) = ab + ac \\ (b + c) \times a = ba + ca \end{aligned}\]
  4. Tertutup

    5. Bilangan riil mempunyai sifat tertutup pada operasi penjumlahan, pengurangan, perkalian maupun pembagian. Misalkan \(a\) dan \(b\) adalah bilangan riil, maka

    \[\begin{aligned} a + b = c \\ a - b = d \\ a \times b = e \\ a \div b = f \end{aligned}\]

    dimana \(c,\) \(d,\) \(e\) dan \(f\) merupakan bilangan riil pula.

  5. Identitas

    6. Bilangan riil mempunyai unsur identitas pada operasi penjumlahan dan perkalian. Untuk setiap bilangan riil \(a\) akan selalu berlaku persamaan

    \[\begin{aligned} a + 0 = a \\ a \times 1 = a \end{aligned}\]

    dimana 0 merupakan unsur identitas pada penjumlahan dan 1 merupakan unsur identitas pada perkalian.

  6. Invers Penjumlahan

    7. Misalkan \(a\) adalah bilangan riil, maka \(a + (-a) = 0.\)

  7. Inverse Perkalian

    8. Misalkan \(a\) adalah bilangan riil, maka \(a \times (1/a) = 1.\)

  8. Perkalian Nol

    9. Setiap bilangan riil dikalikan dengan 0 maka hasilnya adalah 0. Misalkan \(a\) adalah bilangan riil, maka \(a \times 0 = 0.\)

Bilangan Kompleks

Bilangan kompleks (complex numbers) adalah kombinasi dari bilangan riil dan bilangan imajiner, dimana dalam bentuk persamaan \(a + bi,\) bilangan \(a\) dan \(b\) adalah bilangan riil dan \(i\) adalah imajiner. Bilangan kompleks dinotasikan oleh \(\mathbb{C}.\)

Artikel yang berhubungan: